Fuzzy controller may be viewed as universal approximators.
Fuzzy controller theory can be used when the model of a system is unknown or when it is known but it becomes impractical/expensive to adopt an analytical method.
This is the case of highly non-linear systems (from controlling an aircraft in extreme attitude to the classical ball and beam control problem).
In these situations, fuzzy systems provide an approximate "good-enough" solution, starting from linguistic specification only.
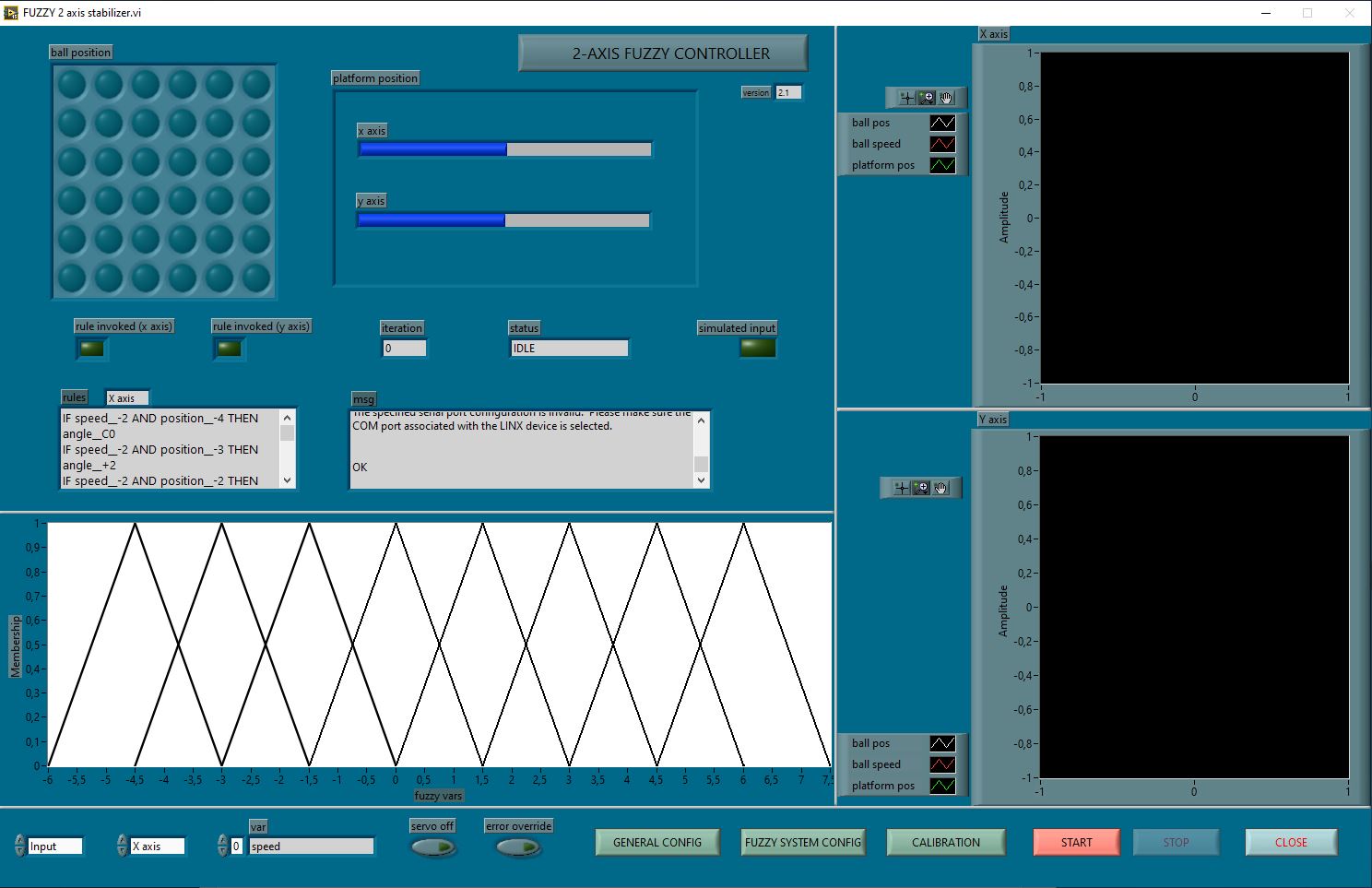
The fuzzy 2-axis controller demonstrator is composed by a platform mounted in a gimbal arrangement, to permit X and Y axis movement. A ball is free to move on the platform. The system must mantain the ball in central position on the platform, regardless any external disturbance.
It would be possibile to solve this problem with a PID regulator or neural networks; here we want to use only linguistic statements, with very little knowledge about the system.
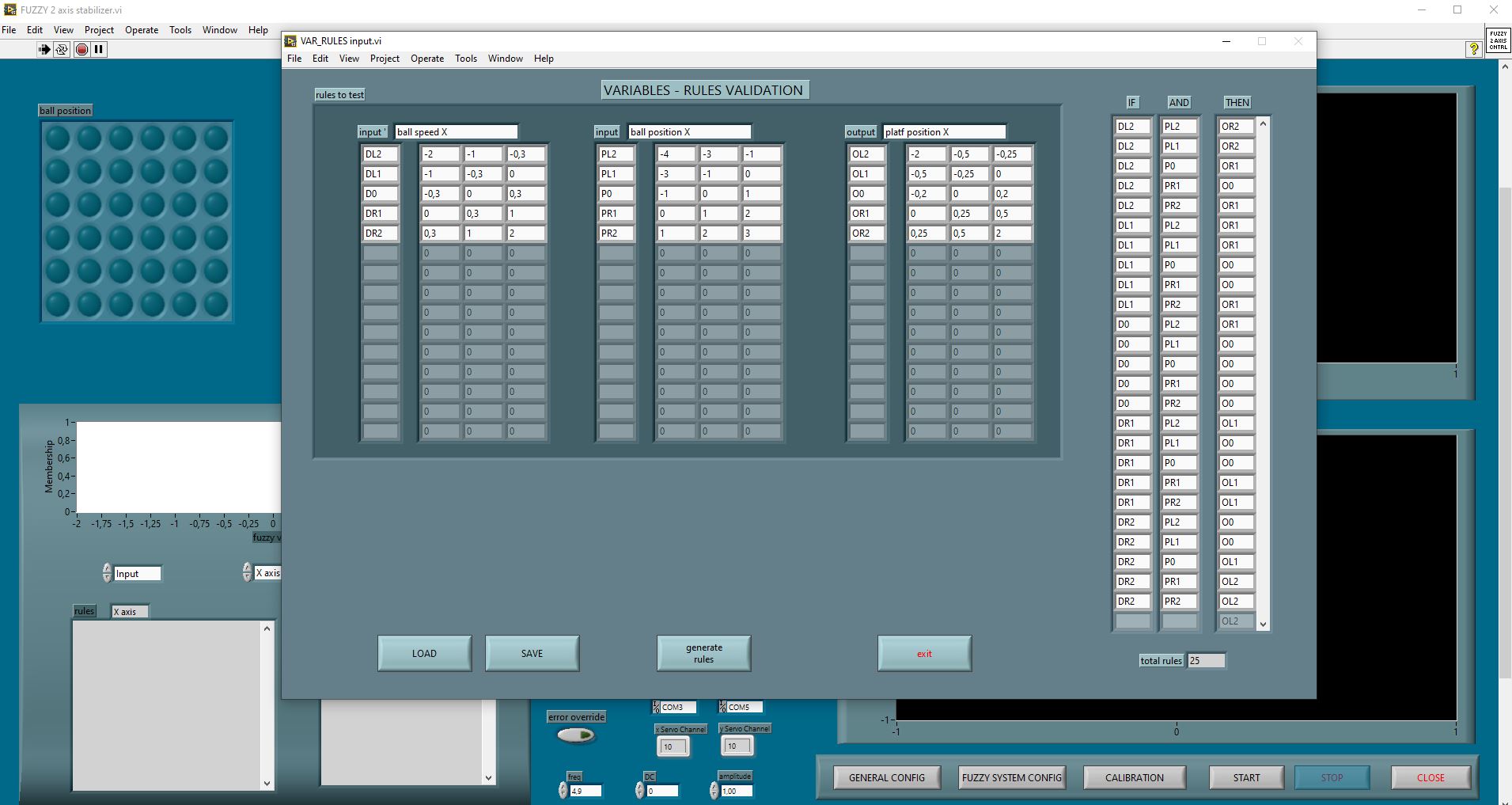
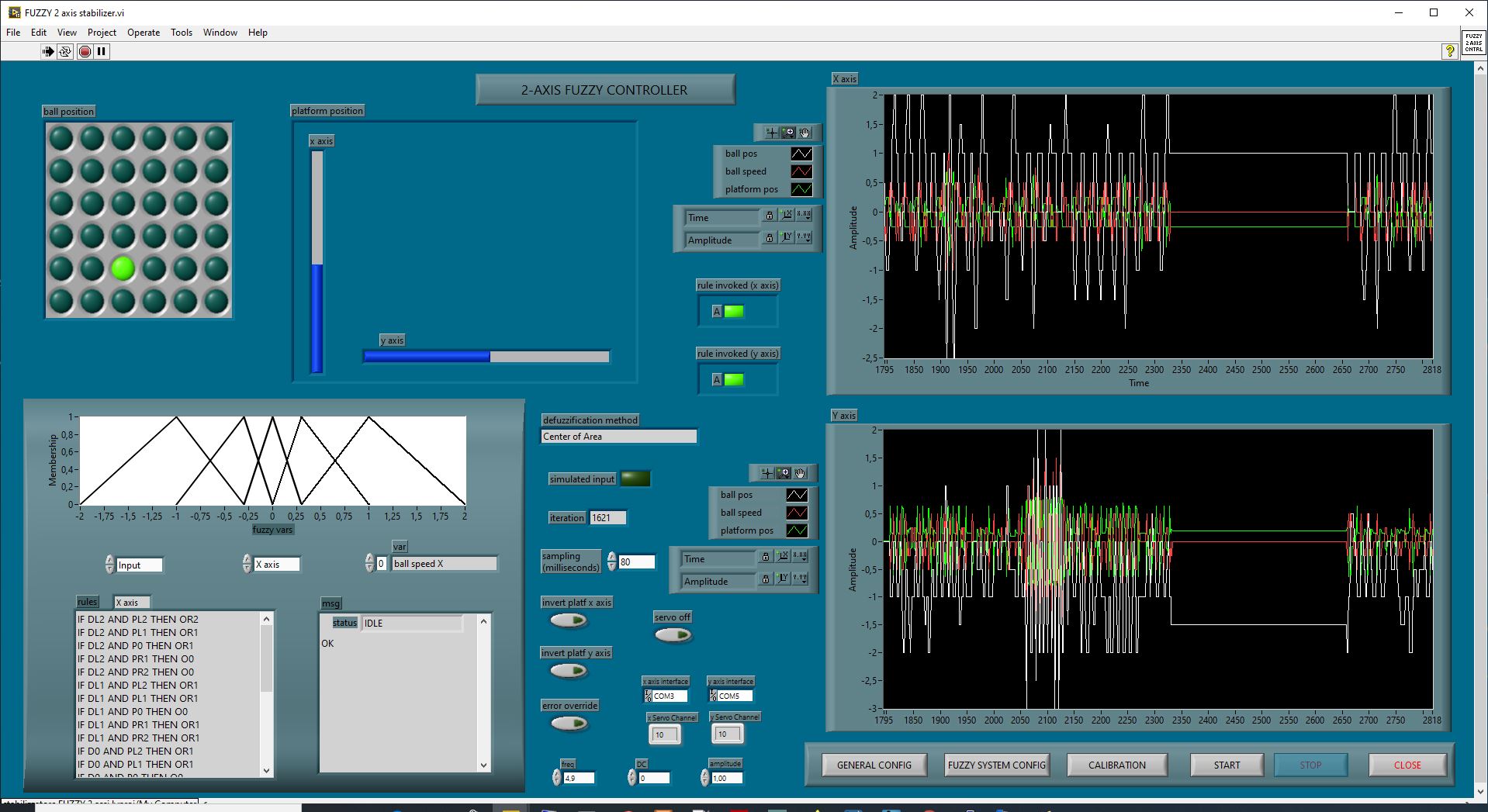
Actually, the system is composed by two distinct controllers (X and Y axis). Ball position and speed are read by a IR grid (below) that provides input to the fuzzy controllers. Output signals drive two RC servos for platform movement.
The IR grid is powered by a low duty cycle pulse current, so to minimize thermal dissipation; pulses are synchronized with software reading of ball position. Position signal is derived to provide ball speed data.
This system is programmed using "IF x(AND y) THEN z" rules. In each rule, x,y and z are set of values (x: ball speed, y: ball position, z: platform angle). These sets are designed so to have some of their intersections not null; so, many rules can be fired at the same time but with different effect percentages, depending on the particular input values.
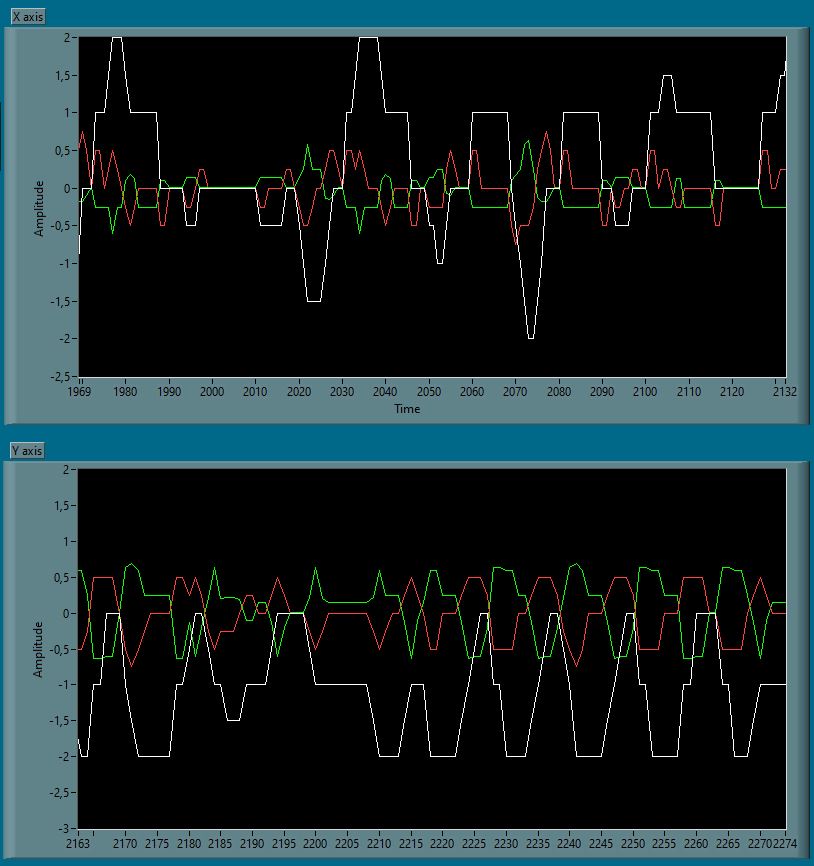
By raising the number of rules, we can observe a better behaviour, but we need greater computational power. Raising the number of the rules too much over a certain threshold doesn't carry improvements, cause the system is limited by sensor resolution and hardware speed.
.png)